How To Solve Japanese Crosswords with Python, Rust, And WebAssembly
How to make a nonogram solver in Python, rewrite it on Rust to run directly in a browser through WebAssembly
One of the most common points of view is that only the correct ones can be called “correct” crossword puzzles. Usually, this is how a solution method is called, in which the dependencies between different rows and/or columns are not taken into account. In other words, a solution is a sequence of independent decisions of individual rows or columns, until all cells are painted over (for more details about the algorithm, see below). For example, only such nonograms can be found at http://nonograms.org
However, it is possible to extend the concept of nonograms to a more general problem, when the usual “logical” method leads to a dead end. In such cases, to solve, you have to make an assumption about the color of a cell and then, having proved that this color leads to a contradiction, mark the opposite color for this cell. The sequence of such steps can (if there is enough patience) give us all the solutions. About solving such a more general case of crossword puzzles and will be mainly this article.
Python
About a year and a half ago, I accidentally stumbled upon an article in which I was told how to solve a single line (as it turned out later, the method was rather slow).
When I implemented this method in Python (my main working language) and added a sequential update of all lines, I saw that all of this was not solved very quickly. After studying the material, it turned out that there are a lot of works and implementations on this topic that offer different approaches for this task.
- It seemed to me that the most extensive work on the analysis of various implementations of solvers was done by Jan Wolter, publishing on his website (which, as far as I know, remains the largest public repository of nonograms on the Internet) a detailed study containing a huge amount of information and links that can help to create your solver.
Studying numerous sources (will be at the end of the article), I gradually improved the speed and functionality of my solver. As a result, I was dragged out and I was engaged in the implementation, refactoring, debugging algorithms for about 10 months in the working time.
Basic algorithms
The resulting solver can be represented in the form of four levels of the solution:
(line) linear solver: at the input, a line of cells and a line of description (clues), at the output – a partially solved line. In the python solution, I implemented 4 different algorithms (3 of them are adapted for color crosswords). The fastest was the BguSolver algorithm, named after the original source. This is a very effective and actually standard method for solving nonogram strings using dynamic programming. Pseudocode of this method can be found for example in this article.
(propagation) we add all the rows and columns to the queue, we pass through it with a linear solver, when we receive new information when we solve the row (column) we update the queue, respectively, with new columns (rows). We continue until the queue is empty.
Example of code:
</p> <p>def propagation(board):<br />line_jobs = PriorityDict()</p> <p>for row_index in range(board.height):<br />new_job = (False, row_index)<br />line_jobs[new_job] = 0</p> <p>for column_index in range(board.width):<br />new_job = (True, column_index)<br />line_jobs[new_job] = 0</p> <p>for (is_column, index), priority in line_jobs.sorted_iter():<br />new_jobs = solve_and_update(board, index, is_column)</p> <p>for new_job in new_jobs:<br /># upgrade priority<br />new_priority = priority - 1<br />line_jobs[new_job] = new_priority</p> <p>def solve_and_update(board, index, is_column):<br />if is_column:<br />row_desc = board.columns_descriptions[index]<br />row = tuple(board.get_column(index))<br />else:<br />row_desc = board.rows_descriptions[index]<br />row = tuple(board.get_row(index))</p> <p>updated = line_solver(row_desc, row)</p> <p>if row != updated:<br />for i, (pre, post) in enumerate(zip(row, updated)):<br />if _is_pixel_updated(pre, post):<br />yield (not is_column, i)</p> <p>if is_column:<br />board.set_column(index, updated)<br />else:<br />board.set_row(index, updated)</p> <p>
- (probing) for each unresolved cell, we search through all the color options and try propagation with this new information. If we get a contradiction, we throw this color out of the color options for the cell and try to benefit from it again with the help of propagation. If it is solved to the end, we add the solution to the list of solutions but continue to experiment with other colors (there may be several solutions). If we come to a situation where it is impossible to solve further, we simply ignore and repeat the procedure with a different color/cell.
Code:
</p>
<p>def probe(self, cell_state):<br />board = self.board</p>
<p>pos, assumption = cell_state.position, cell_state.color<br /># already solved<br />if board.is_cell_solved(pos):<br />return False</p>
<p>if assumption not in board.cell_colors(pos):<br />LOG.warning("The probe is useless: color '%s' already unset", assumption)<br />return False</p>
<p>save = board.make_snapshot()</p>
<p>try:<br />board.set_color(cell_state)<br />propagation(<br />board,<br />row_indexes=(cell_state.row_index,),<br />column_indexes=(cell_state.column_index,))<br />except NonogramError:<br />LOG.debug('Contradiction', exc_info=True)<br /># rollback solved cells<br />board.restore(save)</p>
<p>else:<br />if board.is_solved_full:<br />self._add_solution()</p>
<p>board.restore(save)<br />return False</p>
<p>LOG.info('Found contradiction at (%i, %i)', *pos)<br />try:<br />board.unset_color(cell_state)<br />except ValueError as ex:<br />raise NonogramError(str(ex))</p>
<p>propagation(<br />board,<br />row_indexes=(pos.row_index,),<br />column_indexes=(pos.column_index,))</p>
<p>return True</p>
<p>
(backtracking) if, when probing, we do not ignore the partially solved puzzle, but continue to recursively call the same procedure, we will get backtracking (in other words, a complete detour into the depth of the potential decision tree). Here begins to play a large role, which cell will be selected as the next expansion of the potential solution. A good study on this topic is in this publication.
Code:
</p>
<p>def search(self, search_directions, path=()):<br />"""<br />Return False if the given path is a dead end (no solutions can be found)<br />"""<br />board = self.board<br />depth = len(path)</p>
<p>save = board.make_snapshot()<br />try:<br />while search_directions:<br />state = search_directions.popleft()</p>
<p>assumption, pos = state.color, state.position<br />cell_colors = board.cell_colors(pos)</p>
<p>if assumption not in cell_colors:<br />LOG.warning("The assumption '%s' is already expired. "<br />"Possible colors for %s are %s",<br />assumption, pos, cell_colors)<br />continue</p>
<p>if len(cell_colors) == 1:<br />LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally',<br />pos, assumption)</p>
<p>try:<br />self._solve_without_search()<br />except NonogramError:<br />LOG.warning(<br />"The last possible color '%s' for the cell '%s' "<br />"lead to the contradiction. "<br />"The path %s is invalid", assumption, pos, path)<br />return False</p>
<p>if board.is_solved_full:<br />self._add_solution()<br />LOG.warning(<br />"The only color '%s' for the cell '%s' lead to full solution. "<br />"No need to traverse the path %s anymore", assumption, pos, path)<br />return True<br />continue</p>
<p>rate = board.solution_rate<br />guess_save = board.make_snapshot()<br />try:<br />LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)',<br />state, depth, rate, path)<br />success = self._try_state(state, path)<br />finally:<br />board.restore(guess_save)</p>
<p>if not success:<br />try:<br />LOG.warning(<br />"Unset the color %s for cell '%s'. Solve it unconditionally",<br />assumption, pos)<br />board.unset_color(state)<br />self._solve_without_search()<br />except ValueError:<br />LOG.warning(<br />"The last possible color '%s' for the cell '%s' "<br />"lead to the contradiction. "<br />"The whole branch (depth=%d) is invalid. ", assumption, pos, depth)<br />return False</p>
<p>if board.is_solved_full:<br />self._add_solution()<br />LOG.warning(<br />"The negation of color '%s' for the cell '%s' lead to full solution. "<br />"No need to traverse the path %s anymore", assumption, pos, path)<br />return True<br />finally:<br /># do not restore the solved cells on a root path - they are really solved!<br />if path:<br />board.restore(save)</p>
<p>return True</p>
<p>def _try_state(self, state, path):<br />board = self.board<br />full_path = path + (state,)</p>
<p>probe_jobs = self._get_all_unsolved_jobs(board)<br />try:<br /># update with more prioritized cells<br />for new_job, priority in self._set_guess(state):<br />probe_jobs[new_job] = priority</p>
<p>__, best_candidates = self._solve_jobs(probe_jobs)<br />except NonogramError as ex:<br />LOG.warning('Dead end found (%s): %s', full_path[-1], str(ex))<br />return False</p>
<p>rate = board.solution_rate<br />LOG.info('Reached rate %.4f on %s path', rate, full_path)</p>
<p>if rate == 1:<br />return True</p>
<p>cells_left = round((1 - rate) * board.width * board.height)<br />LOG.info('Unsolved cells left: %d', cells_left)</p>
<p>if best_candidates:<br />return self.search(best_candidates, path=full_path)</p>
<p>return True</p>
<p>
So, we begin to solve our crossword puzzle from the second level (the first one is suitable only for a degenerate case when there is only one row or column in the whole crossword puzzle) and gradually move up the levels. As you might guess, each level several times causes the underlying level, so for an effective solution, it is extremely necessary to have fast first and second levels, which can be called millions of times for complex puzzles.
At this stage, it turns out (quite expectedly) that python is not at all the tool that is suitable for maximum performance in such a CPU-intensive task: all the calculations in it are extremely inefficient compared to lower-level languages. For example, the most algorithmically close BGU-solver (in Java) was 7–17 (sometimes up to 27) times faster on a variety of tasks.
And this is already after I started using PyPy, and on standard CPython, the calculation time was 4-5 times higher than on PyPy! We can say that the performance of a similar Java solver turned out to be higher than CPython code by 28-85 times.
Attempts to improve the performance of my solver with the help of profiling (cProfile, SnakeViz, line_profiler) led to some acceleration, but they certainly didn’t give a supernatural result.
Results:
- The solver can solve all puzzles from https://webpbn.com, http://nonograms.org and it’s own (ini-based) format
- Solves black-and-white and colored nonograms with any number of colors (the maximum number of colors that was encountered is 10)
- Solves puzzles with missing block sizes (blotted). An example of such a puzzle.
- Able to render puzzles to the console/curses window/browser (when installing the additional option pynogram-web). For all modes, viewing the progress of the solution in real time is supported.
- Slow calculations (compared to the implementations described in the article-comparison of solvers, see table).
- Ineffective backtracking: some puzzles can be solved for hours (when the decision tree is very large).
Rust
Earlier this year, I began to study Rust. I started, as usual, with The Book, I learned about WASM, I went through the proposed tutorial. However, I wanted some real task in which the strengths of the language could be acted upon (first of all, its super-performance) and not examples invented by someone. So I went back to the nonograms. But now I already had a working version of all the algorithms in Python, it remains “only” to rewrite.
From the very beginning, the good news was waiting for me: it turned out that Rust, with its type system, perfectly describes the data structures for my task. For example, one of the basic matches BinaryColor + BinaryBlock / MultiColor + ColoredBlock allows you to permanently separate black and white and colored nonograms. If somewhere in the code we try to solve a color string using ordinary binary description blocks, we get a compilation error about the type mismatch.
Base types look like this:
</p>
<p>pub trait Color<br />{<br />fn blank() -> Self;<br />fn is_solved(&self) -> bool;<br />fn solution_rate(&self) -> f64;</p>
<p>fn is_updated_with(&self, new: &Self) -> Result<bool, String>;</p>
<p>fn variants(&self) -> Vec<Self>;<br />fn as_color_id(&self) -> Option<ColorId>;<br />fn from_color_ids(ids: &[ColorId]) -> Self;<br />}</p>
<p>pub trait Block<br />{<br />type Color: Color;</p>
<p>fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self {<br />let size = s.parse::<usize>().expect("Non-integer block size given");<br />Self::from_size_and_color(size, color)<br />}</p>
<p>fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self;</p>
<p>fn size(&self) -> usize;<br />fn color(&self) -> Self::Color;<br />}</p>
<p>#[derive(Debug, PartialEq, Eq, Hash, Clone)]<br />pub struct Description<T: Block><br />where<br />T: Block,<br />{<br />pub vec: Vec<T>,<br />}</p>
<p>// for black-and-white puzzles</p>
<p>#[derive(Debug, PartialEq, Eq, Hash, Copy, Clone, PartialOrd)]<br />pub enum BinaryColor {<br />Undefined,<br />White,<br />Black,<br />BlackOrWhite,<br />}</p>
<p>impl Color for BinaryColor {<br />// omitted<br />}</p>
<p>#[derive(Debug, PartialEq, Eq, Hash, Default, Clone)]<br />pub struct BinaryBlock(pub usize);</p>
<p>impl Block for BinaryBlock {<br />type Color = BinaryColor;<br />// omitted<br />}</p>
<p>// for multicolor puzzles</p>
<p>#[derive(Debug, PartialEq, Eq, Hash, Default, Copy, Clone, PartialOrd, Ord)]<br />pub struct MultiColor(pub ColorId);</p>
<p>impl Color for MultiColor {<br />// omitted<br />}</p>
<p>#[derive(Debug, PartialEq, Eq, Hash, Default, Clone)]<br />pub struct ColoredBlock {<br />size: usize,<br />color: ColorId,<br />}</p>
<p>impl Block for ColoredBlock {<br />type Color = MultiColor;<br />// omitted<br />}</p>
<p>
When migrating the code, some moments clearly indicated that a statically typed language, such as Rust (or, for example, C ++), is more suitable for this task. More precisely, generics and traits describe the subject area better than class hierarchies. So in the Python code, I had two classes for a linear solver, BguSolver and BguColoredSolver, which decided, respectively, the black-and-white line and the color line. In the Rust code, I still have a single generic structure struct DynamicSolver <B: Block, S = <B as Block>:: Color>, which can solve both types of tasks, depending on the type transferred during creation (DynamicSolver <BinaryBlock>, DynamicSolver <ColoredBlock>). This, of course, does not mean that something similar cannot be done in Python, just in Rust, the type system explicitly pointed out to me that if you do not go this way, you will have to write a ton of duplicate code.
In addition, anyone who tried to write on Rust undoubtedly noticed the effect of “trusting” the compiler, when the process of writing code reduces to the following pseudo-meta-algorithm:
When the compiler stops issuing errors and warnings, your code will be coordinated with the type system and borrow checker and you will warn in advance of a heap of potential bugs (of course, subject to the careful design of data types).
I will give a couple of examples of functions that show how concise Rust code can be (compared to Python analogs).
Unsolved_neighbours:
</p>
<p>def unsolved_neighbours(self, position):<br />for pos in self.neighbours(position):<br />if not self.is_cell_solved(*pos):<br />yield pos</p>
<p>fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ {<br />self.neighbours(&point)<br />.into_iter()<br />.filter(move |n| !self.cell(n).is_solved())<br />}</p>
<p>
Partial_sums
</p>
<p>@expand_generator<br />def partial_sums(blocks):<br />if not blocks:<br />return</p>
<p>sum_so_far = blocks[0]<br />yield sum_so_far</p>
<p>for block in blocks[1:]:<br />sum_so_far += block + 1<br />yield sum_so_far</p>
<p>fn partial_sums(desc: &[Self]) -> Vec<usize> {<br />desc.iter()<br />.scan(None, |prev, block| {<br />let current = if let Some(ref prev_size) = prev {<br />prev_size + block.0 + 1<br />} else {<br />block.0<br />};<br />*prev = Some(current);<br />*prev<br />})<br />.collect()<br />}</p>
<p>
When porting, I made a few changes.
the core of the solver (algorithms) has undergone minor changes (primarily to support generic types for cells and blocks)
left the only (fastest) algorithm for linear solver
instead of ini format introduced a slightly modified TOML format
did not add support for blotted crosswords, because, strictly speaking, this is a different class of tasks
left the only way out – just to the console, but now the colored cells in the console are drawn really colored (thanks to this create)
Example:

Useful tools
- Clippy – a standard static analyzer, which sometimes can even give tips that slightly increase code performance
- Valgrind is a tool for dynamic analysis of applications. I used it as a profiler to search for bottlenecks (Valgrind –tool = callgrind) and especially voracious parts of the code (Valrgind –tool = massif). Tip: set [profile.release] debug = true in Cargo.toml before running the profiler. This will leave the debug characters in the executable file.
- kcachegrind for viewing callgrind files. A very useful tool for finding the most problematic places in terms of performance.
Performance
That, for the sake of what and was started rewriting on Rust. We take crosswords from the already mentioned comparison table and run them through the best solvers described in the original article. Results and description of the runs here. We take the resulting file and build a couple of graphs on it. Since the solution time varies from milliseconds to tens of minutes, the graph is executed with a logarithmic scale.
Run on a Jupiter laptop:
</p>
<p>import pandas as pd<br />import numpy as np<br />import matplotlib.pyplot as plt<br />%matplotlib inline</p>
<p># strip the spaces<br />df = pd.read_csv('perf.csv', skipinitialspace=True)<br />df.columns = df.columns.str.strip()<br />df['name'] = df['name'].str.strip()</p>
<p># convert to numeric<br />df = df.replace('\+\ *', np.inf, regex=True)<br />ALL_SOLVERS = list(df.columns[3:])<br />df.loc[:,ALL_SOLVERS] = df.loc[:,ALL_SOLVERS].apply(pd.to_numeric)<br /># it cannot be a total zero<br />df = df.replace(0, 0.001)<br />#df.set_index('name', inplace=True)</p>
<p>SURVEY_SOLVERS = [s for s in ALL_SOLVERS if not s.endswith('_my')]<br />MY_MACHINE_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] in SURVEY_SOLVERS]<br />MY_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] not in SURVEY_SOLVERS]</p>
<p>bar_width = 0.17<br />df_compare = df.replace(np.inf, 10000, regex=True)<br />plt.rcParams.update({'font.size': 20})</p>
<p>def compare(first, others):<br />bars = [first] + list(others)<br />index = np.arange(len(df)) <br />fig, ax = plt.subplots(figsize=(30,10))</p>
<p>df_compare.sort_values(first, inplace=True)</p>
<p>for i, column in enumerate(bars):<br />ax.bar(index + bar_width*i, df_compare[column], bar_width, label=column[:-3])</p>
<p>ax.set_xlabel("puzzles")<br />ax.set_ylabel("Time, s (log)")<br />ax.set_title("Compare '{}' with others (lower is better)".format(first[:-3]))<br />ax.set_xticks(index + bar_width / 2)<br />ax.set_xticklabels("#" + df_compare['ID'].astype(str) + ": " + df_compare['name'].astype(str))<br />ax.legend()</p>
<p>plt.yscale('log')<br />plt.xticks(rotation=90)<br />plt.show()<br />fig.savefig(first[:-3] + '.png', bbox_inches='tight')</p>
<p>for my in MY_SOLVERS:<br />compare(my, MY_MACHINE_SOLVERS)</p>
<p>compare(MY_SOLVERS[0], MY_SOLVERS[1:])</p>
<p>
Python solver

We see that the pynogram here is the slowest of all represented solvers. The only exception to this rule is the Tamura / Copris solver, based on the SAT, which solves the simplest puzzles (left part of the graph) longer than ours. However, such is the peculiarity of SAT-solvers: they are designed for super complex crosswords, in which an ordinary solver is stuck in backtracking for a long time. This is clearly visible on the right side of the chart, where Tamura/Copris solves the most difficult puzzles tens and hundreds of times faster than any other.
Rust solder
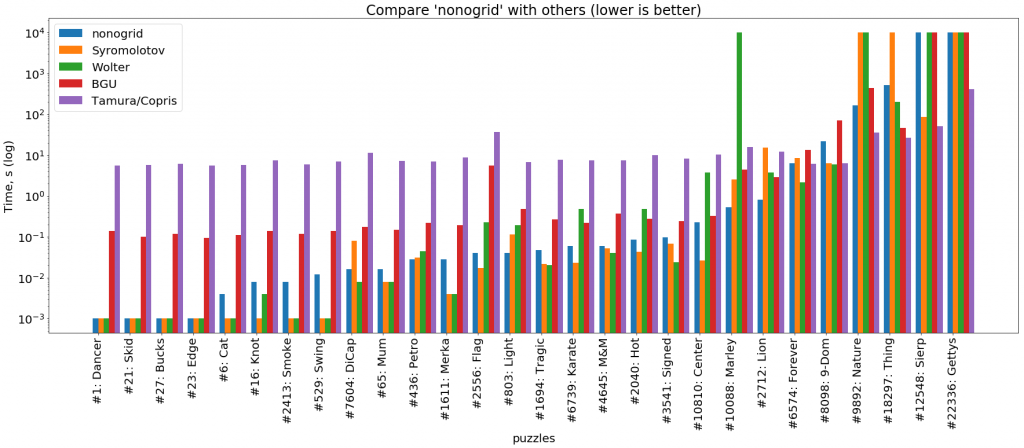
This graph shows that nonogrid copes with simple tasks as well or slightly worse than high-performance solvers written in C and C ++ (Wolter and Syromolotov). With the complication of tasks, our solver roughly repeats the trajectory of a BGU-solver (Java), but almost always advances it by an order of magnitude. On the most difficult tasks, Tamura / Copris is always ahead of everyone.
Rust vs Python

Well, finally, a comparison of our two solvers, described here. It can be seen that the Rust-solver almost always leads by 1-3 orders of magnitude to the Python solver.
Results:
- The solver can solve all puzzles from https://webpbn.com (except blotted – with partially hidden block sizes), http://nonograms.org and its own (TOML-based) format
- Solves black-and-white and color nonograms with any number of colors
- Knows how to render puzzles to the console (color c webpbn.com draws truly color)
- It works quickly (in comparison with the implementations described in the article-comparison of solvers, see table).
Backtracking remained ineffective, as in the Python solution: some puzzles (for example, such a harmless 20×20) can be solved for hours (when the decision tree is very large). Perhaps instead of backtracking, you should use the SAT-solvers already mentioned in the SmartSpate. True, the only SAT-solver I found on Rust at first glance seems to be underdeveloped and abandoned.
WebAssembly
So, rewriting the code to Rust has borne fruit: the solver has become much faster. However, Rust offers us another incredibly cool feature: compiling to WebAssembly and the ability to run your code directly in the browser.
To implement this feature, there is a special tool for Rust, which provides the necessary binders and generates a boilerplate for you to run Rust functions smoothly in the JS code – this wasm-pack (+ wasm-bindgen). Most of the work with it and other important tools is already described in the Rust and WebAssembly tutorial. However, there are a couple of things that I had to figure out on my own:
- Reading gives the impression that the tutorial is primarily written for a JS developer who wants to speed up his code with Rust. Or at least for someone who is familiar with npm. For me, as a person far from the front-end, it was a surprise to discover that even the standard book example does not want to work with a third-party web server different from npm run start.
Fortunately, the wasm-pack has a mode that allows you to generate a regular JS code (which is not an npm module). wasm-pack build – target no-modules – a no-typescript will yield only two files at the output: project-name.wasm – Rust-code binary compiled in WebAssembly and project-name.js. You can add the latest file to any HTML <script src = “project-name.js”> </ script> page and use WASM functions without bothering with npm, webpack, ES6, modules and other joys of a modern JS developer. The no-modules mode is ideal for non-front-enders during the development of a WASM application, as well as for examples and demonstrations because it does not require any additional front-end infrastructure.
- WebAssembly is good for tasks that are too heavy for javascript. First of all, these are tasks that perform many calculations. And if so, this task can be performed for a long time even with WebAssembly and thus violate the asynchronous principle of the modern web. I’m talking about all sorts of Warning: Unresponsive script, which I happened to observe while working my solver. To solve this problem, you can use the mechanism of Web worker. In this case, the scheme of work with “heavy” WASM-functions may look like this:
- From the main script of the event (for example, clicking on a button) send a message to the worker with the task to start a heavy function.
- The worker accepts the task, starts the function and returns the result when it ends.
- The main script accepts the result and somehow processes it (renders)
When creating a WASM interface, it is not possible to transfer all created data types to JS, and this is contrary to the practice of using WASM. However, between calls to functions, you need to somehow store the state (an internal representation of nonograms describing cells and blocks), so I used the global HashMap to store nonograms by their sequence numbers, which is not visible from the outside. When querying from the outside (from JS), only the number of the crossword puzzle is transferred, after which the crossword itself is then restored to launch the solution/query the solution results.
To ensure safe access to the global dictionary, it wraps itself in Mutex, which forces all structures to be replaced with thread-safe. Changes, in this case, relate to the use of smart pointers in the main code of the solver. To support thread-safe operations, I had to replace all Rc with Arc and RefCell with rwlock. However, this operation immediately affected the performance of the solver: the execution time, by the most optimistic estimate, increased by 30%. To bypass this restriction, I added a special option – features = threaded if necessary to use a solver in a thread-safe environment, which is necessary for the WASM interface.
As a result of the measurements made on crosswords 6574 and 8098, the following result was obtained (the best time in seconds out of 10 starts):

It can be seen that in the web interface the puzzle is solved by 40..70% slower than when launching a native application in the console, and most of this slowdown (32..37%) takes up the launch in thread-safe mode (cargo build – -release –features = threaded).
Tests were conducted in Firefox 67.0 and Chromium 74.0.
WASM-solver can be tried here (source). The interface allows you to select a crossword puzzle by its number from one of the sites https://webpbn.com/ or http://www.nonograms.org/
Todo
- “discarding” solved rows/columns to facilitate/speed up the decision at the backtracking stage.
- If the solver finds several solutions, the interface does not show them. Instead, it shows the most “general” solution, that is, an incomplete solution, in which open cells may have different meanings. It is necessary to add a display of all the solutions found.
- There is no time limit (some puzzles are considered very long, traditionally I ran with a timeout of 3600 seconds). In WASM, it is impossible to use the time system call to start the limiting timer (in fact, this is the only (!) Change that had to be made in order for the solver to work in WASM). This, I am sure, can somehow be fixed, but it may be necessary to make changes in the main nonogrid kit.
- Impossible to track progress. Here I have some developments: callbacks that can work when cells change state, but I have not thought about how to forward them in WASM. It may be worthwhile to create a queue tied to the puzzle and write all (or major) changes to it at the decision stage, and from the JS side to make a cycle reading this queue and rendering changes.
- Error notifications in js. For example, when requesting a non-existent puzzle, a backtrace falls into the console, but nothing happens on the page.
- Add support for other sources and external nonograms (for example, the ability to upload files in TOML format)
Results
- The problem of solving nonograms allowed me to gain a ton of new knowledge about algorithms, languages, and infrastructure (profilers, analyzers, etc).
- Solver on Rust is 1–3 orders of magnitude faster than Solver on PyPy with an increase in the amount of code by only 1.5–2 times (it did not measure exactly).
- Porting code from Python to Rust is quite simple if it is broken down into fairly small functions and uses Python functionality (iterators, generators, comprehensions) that are remarkably translated into idiomatic Rust code.
- You can write on Rust under WebAssembly now. At the same time, the performance of the execution of the Rust code compiled in WASM is rather close to the native application (on my task it is about 1.5 times slower).